#문제
https://www.acmicpc.net/problem/2749
2749번: 피보나치 수 3
첫째 줄에 n이 주어진다. n은 1,000,000,000,000,000,000보다 작거나 같은 자연수이다.
www.acmicpc.net
#작성 코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
|
#include <iostream>
#include <vector>
using namespace std;
long long int n;
int mod = 1000000;
vector<vector<long long int> > one(2, vector<long long int>(2));
vector<vector<long long int> > matmul(vector<vector<long long int> > a, vector<vector<long long int> > b){
int size = a.size();
vector<vector<long long int> > result(size, vector<long long int>(size));
for(int i=0; i<size; i++){
for(int j=0; j<size; j++){
for(int k=0; k<size; k++){
result[i][j]+=(a[i][k]*b[k][j])%mod;
}
result[i][j]%=mod;
}
}
return result;
}
vector<vector<long long int> > matpow(vector<vector<long long int> > a, long long int b){
if( b==0 ){
return one;
}
else if(b==1){
return a;
}
else if(b%2==0){
vector<vector<long long int> > tmp = matpow(a, b/2);
return matmul(tmp, tmp);
}
else{
vector<vector<long long int> > tmp = matpow(a, b-1);
return matmul(a, tmp);
}
}
int main(){
cin>>n;
one[0][0]=1; one[1][1]=1;
vector<vector<long long int> > mat(2, vector<long long int>(2));
mat[0][0]=mat[0][1]=mat[1][0]=1;
mat[1][1]=0;
vector<vector<long long int> > result(2, vector<long long int>(2));
result = matpow(mat, n);
cout<<result[0][1]%mod<<'\n';
return 0;
}
|
cs |
##
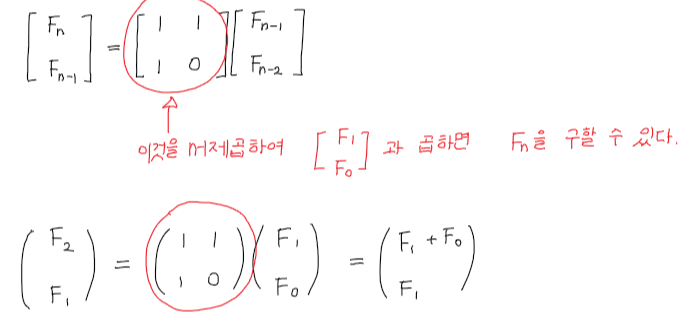
앞서 풀었던 10830 행렬 제곱 문제와 동일한 풀이로 풀 수 있었다.
행렬 제곱을 응용하지 않고, '피사노 주기'라는 것을 이용하면 더 수월하게 풀 수 있다.
* 피사노 주기

주기를 구하는 함수를 만든다면, 항상 F(0) = 0, F(1) = 1임을 이용한다. 0과 1이 반복되는 구간을 찾으면 그 구간이 주기가 된다.
주기를 찾는다면 그 주기만큼의 피보나치 수를 메모이제이션으로 구하고, n번째 피보나치 수 % k는 (n%주기길이) 번째 피보나치 수를 %k 연산하면 된다.
피보나치 수를 구하는 방법에 대해 참고하면 좋을만한 글을 발견했다!
참고 :https://www.acmicpc.net/blog/view/28
피보나치 수를 구하는 여러가지 방법
피보나치 수는 다음과 같이 정의되는 수열입니다. $F_0 = 0$ $F_1 = 1$ $F_n = F_{n-1} + F_{n-2}$ 피보나치 수를 조금 써보면, 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... 와 같습니다. 피보나치 수를 구하는 함수를 작성해보고 10870번 문제: 피보나치 수 5를 풀어보겠습니다. #include using namespace std; int fibonacci(int n) { if (
www.acmicpc.net
'BOJ' 카테고리의 다른 글
| BOJ 10866번 :: 덱 (0) | 2019.12.28 |
|---|---|
| BOJ 1654번 :: 랜선 자르기 (0) | 2019.12.28 |
| BOJ 10830번 :: 행렬 제곱 (0) | 2019.12.27 |
| BOJ 10816번 :: 숫자 카드 2 (0) | 2019.12.27 |
| BOJ 1966번 :: 프린터 큐 (0) | 2019.12.27 |