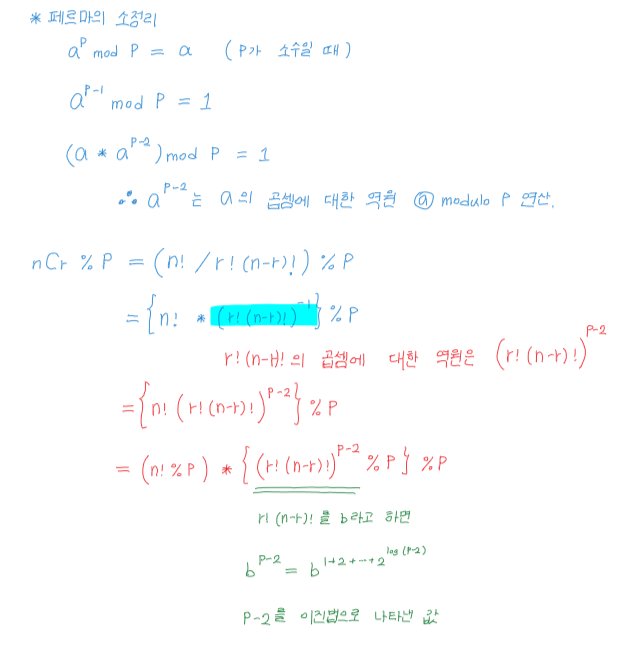#문제
https://www.acmicpc.net/problem/1874
1874번: 스택 수열
1부터 n까지에 수에 대해 차례로 [push, push, push, push, pop, pop, push, push, pop, push, push, pop, pop, pop, pop, pop] 연산을 수행하면 수열 [4, 3, 6, 8, 7, 5, 2, 1]을 얻을 수 있다.
www.acmicpc.net
#작성 코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
#include <iostream>
#include <queue>
#include <stack>
using namespace std;
int nums[100000];
// c/c++에서는 a[100000] 크기의 배열을 지역변수로 선언할 수 없다고해서 전역변수로 선언
int main(){
int n;
cin>>n;
for(int i=0; i<n; i++){
cin>>nums[i]; // 인덱스 1~n 사용
}
// 1~n의 수열을 만들어보자
// 스택에 push 하는 순서는 반드시 오름차순을 지킨다
// 임의의 수열을 스택을 이용해 그 수열을 만들 수 있으면push/pop연산 출력해서 표현하고
// 만들수없으면 NO를 출력한다.
stack<int> st;
queue<char> q;
int i=1, j=0;
while( j<n ){
// 스택이 비어있지않고 top==nums[j]일때
while( !st.empty() && st.top() == nums[j] ){
st.pop();
q.push('-');
j++;
}
// nums[j]까지의 수(i)를 스택에 push한다.
if( nums[j]>=i ){
while(true){
if( nums[j]<i ) break;
st.push(i);
q.push('+');
i++;
}
}
// nums[j]까지의 수가 이미 스택에 들어갔는데
// 스택이 비어있지않고, top에 존재하는 수가 nums[j]보다 크다면
// 이 수열은 스택을 이용해서 만들 수 없으므로 NO를 출력
else if( !st.empty() && st.top()>nums[j] ){
cout<<"NO\n";
return 0;
}
}
while(!q.empty()){
cout<<q.front()<<'\n';
q.pop();
}
return 0;
}
|
cs |
아래 코드처럼 수정하니 조금 더 깔끔한것같다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 | #include <iostream> #include <queue> #include <stack> using namespace std; int nums[100000]; // c/c++에서는 a[100000] 크기의 배열을 지역변수로 선언할 수 없다고해서 전역변수로 선언 int main(){ int n; cin>>n; for(int i=0; i<n; i++){ cin>>nums[i]; // 인덱스 1~n 사용 } // 1~n의 수열을 만들어보자 // 스택에 push 하는 순서는 반드시 오름차순을 지킨다 // 임의의 수열을 스택을 이용해 그 수열을 만들 수 있으면push/pop연산 출력해서 표현하고 // 만들수없으면 NO를 출력한다. stack<int> st; queue<char> q; // '+'와 '-'를 저장한다. int i=1, j=0; // 1부터 n까지의 수를 차례로 스택에 push하면서 // 수열 현재값과 같으면 스택에서 pop하는 방식으로 비교해나간다. for(int i=1; i<=n; i++){ st.push(i); q.push('+'); // 스택의 최상단과 수열 현재값 같으면 // 비교하고, 스택에서 pop할 수 있는만큼 pop한다 while( !st.empty()&&st.top()==nums[j] ){ st.pop(); q.push('-'); j++; } } // n까지 스택에 push 후에 수열과 같다면 pop하는 방식에서 // 스택에 값이 남아있다면 해당 수열을 스택을 이용해서 만들수없다는 뜻 if( !st.empty() ){ cout<<"NO\n"; return 0; } // 스택이 비어있다면 해당 수열을 만들수 있다는 뜻 // 큐에 저장된 것을 출력한다. else{ while(!q.empty()){ cout<<q.front()<<'\n'; q.pop(); } } return 0; } | cs |
##
int a[100,000] 정도 크기의 배열은 main 함수 내에서 지역 변수로 선언하면 런타임 에러/ 메모리 초과 오류가 발생할 수 있다는 글을 읽고(https://www.acmicpc.net/board/view/32251) 전역 변수로 선언했더니 에러를 해결하고 AC 판정을 받을 수 있었다.
'BOJ' 카테고리의 다른 글
| BOJ 11866번 :: 조세퍼스 문제 0 (0) | 2019.12.26 |
|---|---|
| BOJ 17298번 :: 오큰수 (0) | 2019.12.26 |
| BOJ 2740번 :: 행렬 곱셈 (0) | 2019.12.25 |
| BOJ 11401번 :: 이항 계수 3 (0) | 2019.12.25 |
| BOJ 1920번 :: 수 찾기 (0) | 2019.12.25 |